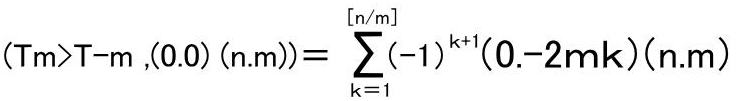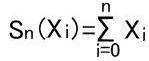
Reflection Principle

　　　Let X1,X2....Xn....be a seqence of independent random variables.

　　　　　　　　　　　　　

　　random walk at time k, the position of the random walk after n step is given by
　　　　　　　　　　　　　

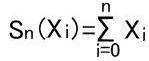
　　　Hitting Times (First passage times)
　　　Let Tk=min{t|St=k} be first hitting times at k.
　　Let us define functions that satisfy the following condition.
　　　　　　　　　　　　　　
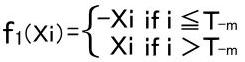
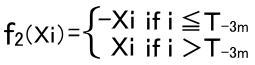
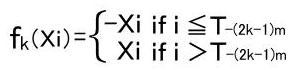
　　　Put (t0.k0)(t1.k1)={s|s=the pass with St1-t0=k1,X0=k0}
　　　　(Tk2>Tk3,(t0.k0)(t1.k1))={s|s=the pass with St1-t0=k1,X0=k0,Tk2>Tk3}
　　The following relation is satisfied.
　　　f1(Tm>T-m,(0.0)(n.m))=(T-m<T-3m,(0.-2m)(n.m))
　　　f2(T-m>T-3m,(0.-2m)(n.m))=(T-3m<T-5m,(0.-4m)(n.m))
　　　fk=(T-(2k-3)m>T-(2k-1)m,(0.-(2k-2)m)(n.m))=(T-(2k-1)m<T-(2k+1)m,(0.-2km)(n.m))
　　　Let us find the total number of following path.
　　　　　　(Tm>T-m,(0.0)(n.m))
　　　The following condition is satisfied.
　　　(0.-2km)(n.m)=(T-(2k-1)m<T-(2k+1)m,(0.2km)(n.m))+(T-(2k-1)m>T-(2k+1)m,(0.2km)(n.m))
　　　The total number of pass 　(Tm>T-m,(0.0)(n.m)) is given by