はじめに、シュペルナーの補題を証明するのに必要なｎ単体と重心細分というものについて説明します。
ｎ単体
ｎ単体とは、ｎ+1個の頂点（（a1,a2,a3------aｎ,an+1)|（a1-ai)(i=1～ｎ+1）が一次独立）から構成されるある領域のことです。例えば、点は0単体であり、線分は1単体で2つの頂点から構成されa1,a2をその頂点とすると
ｂ1a1+ｂ2a2（0≦ｂi≦1|i=1,2）ｂ1+ｂ2＝1。
また、三角形は2単体で3つ頂点a1,a2,a3から構成され
ｂ1a1+ｂ2a2+ｂ3a3（0≦ｂi≦1|i=1,2,3）ｂ1+ｂ2+ｂ3＝1
そしてその頂点を重心細分すれば、ｎ単体を分割することができます。1単体（線分）の重心細分とは線分の中間点に新たに頂点を設け線分を2つの線分に分割することです。
下図は、a1,a2をその頂点とする1単体（線分）の重心細分です。頂点a1,a2の中間に新たに頂点a3が加わり1単体（a1,a2）が1単体（a1,a3）と1単体（a3,a2）に分割されました。
さらに、この1単体（a1,a3）（a3,a2）を重心細分すると、下図の様に頂点a1,a3と頂点a2,a3の中間点それぞれに頂点a4,a5が加わり1単体
（a1,a4）（a4,a3）（a3,a5）（a5,a2）に分割されます。
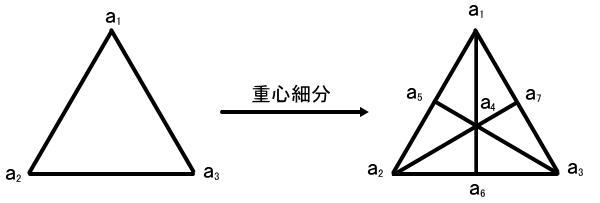
2単体（三角形）の重心細分は、下図の様になります。頂点a1,a2,a3の中間点に頂点a4が頂点a1,a2の中間点に頂点a5が同様にして頂点a6,a7が新たに加
わります。こうして、2単体（a1,a2,a3）が2単体（a1,a4,a5）（a1,a4,a7）（a2,a4,a5）（a2,a4,a6）（a3,a4,a7）（a3,a4,a6）と6つの2単体に分割されました。
次に、一般的なＮ単体の重心細分について説明していきます。
Ｎ単体の重心細分
Ｎ+1個の頂点を（（a1.1,a1.2,a1.3------a1.ｎ,a1.n+1)|（a1.1-a1.i)（i=1～ｎ+1）が一次独立）とします。
そうすると、ｂ1a1.1+ｂ2a1.2+ｂ3a1.3+-----bna1.ｎ+ｂｎ+1a1.n+1（0≦ｂi≦1|i=1～ｎ+1）
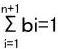この領域がＮ単体となります。以下、重心細分の過程を説明します。
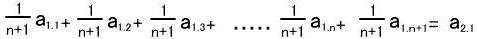この計算により新たに頂点a2.1が生成されました。↓（a1.1,a1.2,a1.3-----a1.n,a1.n+1)からｎ個の頂点を選択する。（ｎ+1通りの場合がありますが、ここでは例としてa1.n+1以外の頂点を選択します。）
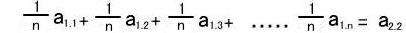この計算により新たに頂点a2.2が生成されました。↓（a1.1,a1.2,a1.3------a1.n)からｎ-1個の頂点を選択する。（ｎ通りの場合がありますが、ここでは例としてa1.n以外の頂点を選択します。）
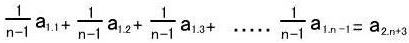この計算により新たに頂点a2.n+3が生成されました。 ↓これを頂点が1つになるまで繰り返す。
・
・
・
↓
(a1.1）
a2.1をＮ単体（a1.1,a1.2,a1.3------a1.n,a1.n+1)の重心といいます。また、（a2.1,a2.2,a2.ｎ+3------a1.1) このＮ+1個の頂点の集合からＮ単体を構成できます。頂点の選択の場合の数は、
（ｎ+1）！通りあるので（a1.1,a1.2,a1.3------a1.n+1)を頂点に持つｎ単体が、その内部に(ｎ+1)！個のｎ単体を含む事になります。
※生成されたaの右下の添字は、左側が何度目の重心細分かを示すもので、Ｎ度目ならばＮ+1を書いています。その右の添字は、どの頂点の集合から生成されたかによって定まります。以下その説明をしていきます。
まず、（a1.1,a1.2,a1.3------a1.n+1)この集合から生成された頂点をa2.1とします。次にＮ個の頂点の集合です。
Ｎ+1個の頂点（a1.1,a1.2,a1.3------a1.n+1）のうちどれか1つが含まれない事になりますが,含まれない頂点a1.iのiが大きいものから順番にまだ使われていない自然数で最小の数を対応させていきます。
例えばa1.n+1を含まない場合（a1.1,a1.2,a1.3------a1.n)＝a2.2 、a1.nを含まない場合(a1.1,a1.2,a1.3------a1.n+1)＝a2.3、a1.1を含まない場合（a1.2,a1.3-----a1.n,a1.n+1)=a2.n+2となります。
そしてＮ-1個の頂点の集合は2つの頂点が含まれない事になりますが、含まれない頂点a1.ia1. j （i＞jとする）のiが大きいものから順番に上の作業でまだ使われていない自然数で最小の数を対応させます。iが同じ集合が、Ｎ個考えられますがそこでは、ｊが大きいものから数を対応させます。
例えばa1.n,a1.n+1を含まない場合（a1.1,a1.2,a1.3------a1.n-2,a1.ｎ-1)＝a2.n+3、a1.n-1,a1.n+1を含まない場合（a1.1,a1.2,a1.3------a1.n-2,a1.ｎ)=a2.n+4となります。
辺単体
ｎ-1辺単体とは、ｎ単体の持つｎ+1個の頂点から選択したｎ個の頂点の集合により構成される単体の事です。
上述重心細分では、1回の重心細分につき(Ｎ+1)！個の新たなｎ単体が生成されますが、これらｎ単体の持つｎ-1辺単体が共通のものとなるのはどの様な場合でしょうか。それは、あるｎ単体の持つ ｎ+1個の頂点のうちｎ個の頂点が他ｎ単体の持つ ｎ+1個の頂点のうちのｎ個の頂点と同じであるという事です。
例 ｎ単体Ａ（a2.1,a2.2,a2.ｎ+3------a1.1) ｎ単体Ｂ（a2.1,a2.3,a2.ｎ+3------a1.1)
ｎ単体Ａとｎ単体Ｂでは、a2.2とa2.3の違いがあります。他の頂点は同じです。つまり、ｎ-1辺単体（a2.1,a2.ｎ+3------a1.1)が共通のものとなっています。ではこの違いはどのようにして生じたのでしょうか。
ここで、ｎ単体Ａとｎ単体Ｂが重心細分によって生成される過程を比較します。
ｎ単体Ａ
1段階目（a1.1,a1.2,a1.3------a1.ｎ,a1.n+1)
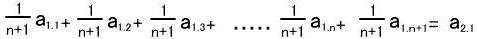
2段階目↓（a1.1,a1.2,a1.3------a1.ｎ,a1.n+1)からｎ個の頂点を選択する。（a1.n+1以外の頂点を選択」します。）
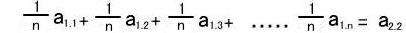
3段階目↓（a1.1,a1.2,a1.3------a1.n) からｎ-1個の頂点を選択する。（a1.n以外の頂点を選択します。）
↓
・
・
・
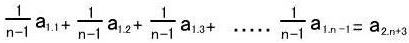
Ｎ+1段階目↓
(a1.1)
ｎ単体Ｂ
1段階目（a1.1,a1.2,a1.3------a1.ｎa1.n+1)
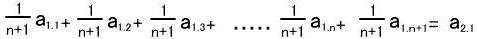
2段階目 ↓（a1.1,a1.2,a1.3------a1.ｎa1.n+1)からｎ個の頂点を選択する。（a1.n以外の頂点を選択」します。）
3段階目↓（a1.1,a1.2,a1.3------a1.n+1) からｎ-1個の頂点を選択する。（a1.n+1以外の頂点を選択します。）
↓
・
・
・
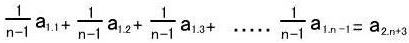
Ｎ段目↓
(a1.1)
このようにｎ+1個の頂点からｎ個の頂点を選択する段階でｎ単体Ａでは、a1.n+1以外をｎ単体Ｂではa1.n以外を選択している。
さらに、次の段階ではｎ単体Ａでは、a1.n以外をｎ単体Ｂではa1.n+1以外を選択している。そしてそれ以後の段階では全て同じ頂点の集合を選択をしている。
ここで、一般的な説明をするために記号の定義をします。
Ｎ単体をσと表記し、最初のσ（a1.1,a1.2,a1.3------a1.n+1）をＳ1と表記します。σ（a1.1,a1.2,a1.3------a1.n+1）＝Ｓ1 さらにＳ1の重心細分によって生成されたＮ+1!個のσの集合をＳ2 、
Ｓ2∋σそれぞれの重心細分によって生成された
個のσの集合をＳ3とし、以下同様にＳi-1の全てのσそれぞれの重心細分によって生成されたσの集合をＳiとする。例えば、σＡ（a2.1,a2.2,a2.ｎ+3------a1.1)∈Ｓ2となります。あるＮ-1個の頂点の集合が、2つの相異なるＮ単体Ｓi∋σｋ、Ｓi∋σｊの頂点の集合に含まれている場合、それぞれのｎ単体が生成される重心細分の過程で、Ｋ-1段階目まで同じ頂点の集合を選択し、ｋ段階目で異なる頂点の集合を選択をしｋ+1段階目からＮ段階目までは、全て同じ頂点の集合を選択をしています。それでは、あるＮ-1個の頂点の集合が3個以上のｎ単体に持たれるということはあり得るでしょうか。
ｎ+1-（ｋ-1）＝ｍとすると ｍ-（ｍ-2）Ｃ（ｍ-1）-（ｍ-2）＝2 組み合わせ論の計算によりあるｎ-1辺単体は、最大でも2つのｎ単体にしか含まれないことがわかります。
ここで、σＡ（a2.1,a2.2,a2.ｎ+3------a1.1)が含むｎ-1辺単体がどのような性質をもつのか詳しくみていきます。
（a2.1,a2.2,a2.n+3------)これは、σＡ（a2.1,a2.2,a2.ｎ+3------a1.1)の持つn個の頂点の集合ですが、これは上述議論によってσＡとは異なるＳ2∋σのｎ個の頂点の集合に含まれます。
一般的に、a2.1を含むｎ個の頂点の集合は、2つの相異なるＮ単体Ｓ2∋σｋ、Ｓ2∋σｊの頂点の集合に含まれます。
逆にa2.1 を含まないｎ個の頂点の集合は1つのＳ2∋σにだけ含まれます。
ここで、Ｓ2∋σそれぞれの重心細分の過程を観察します。
例としてσＡ（a2.1,a2.2,a2.ｎ+3------a1.1) ,σＢ（a2.1,a2.3,a2.ｎ+3------a1.1)の重心細分をみていきます。
σＡ（a2.1,a2.2,a2.ｎ+3------a1.1)
1段階目（a2.1,a2.2,a2.ｎ+3------a1.1)
2段階目↓上のｎ+1個の頂点からｎ個の頂点を選択する。（ここでは、a2.2以外の頂点を選択」します。）
（a2.1,a2.ｎ+3------a1.1)
3段階目↓上の頂点からｎ-1個の頂点を選択する。（ここでは、a2.1以外の頂点を選択します。）
（a2.ｎ+3------a1.1)
・
・
・
Ｎ段階目↓
（a1.1)
σＢ（a2.1,a2.3,a2.ｎ+3------a1.1)
1段階目（a2.1,a2.3,a2.ｎ+3------a1.1)
2段階目↓上のｎ+1個の頂点からｎ個の頂点を選択する。（ここでは、a2.3以外の頂点を選択」します。）
（a2.1,a2.ｎ+3------a1.1)
3段階目↓上の頂点からｎ-1個の頂点を選択する。（ここでは、a2.1以外の頂点を選択します。）
（a2.ｎ+3------a1.1)
・
・
・
Ｎ段階目↓
（a1.1)
2段階目の頂点の選択でσＡ、σＢで相異なる頂点,a2.2 a2.3がそれぞれ取り除かれている。そしてそれ以後は全く同じ頂点の集合を選択している。
Ｓ2∋σの重心細分では、重心細分の2段階目でＮ+1個の頂点の集合からＮ個の頂点を選択しますが、そのＮ 個にa2.1を含む場合と含まない場合があります。
その結果 集合Ｊ＝{Ｓ3∋σ|σ＝自身が生成される過程2段階目でＮ 個の頂点の集合がa2.1を含む}
集合Ｋ＝{Ｓ3∋σ|σ＝自身が生成される過程2段階目でＮ 個の頂点の集合がa2.1含まない}
集合Ｊ,Kをこのように定義すると、Ｓ3は、この2つの集合Ｊ,Ｋの和集合となります。
Ｊ∋σiの任意のＮ個の頂点の集合は、他のあるＳ3∋σkのもつＮ個の頂点の集合と共通のものとなります。今後、この性質を持つσをタイプ1のσと呼ぶことにします。そして、Ｋ∋σiは、自身がもつＮ+1通りのN個の頂点の集合のうちＮ通りは、他のあるＳ3∋σkのもつＮ個の頂点の集合と共通のものとなりますが、一つだけ、自身しか持たないＮ個の頂点の集合があります。今後、この性質を持つσをタイプ2のσと呼ぶことにします。
タイプ1のＳi∋σi,タイプ2のＳi∋σiの定義
タイプ1のＳi∋σi,自身が持つ任意のＮ個の頂点の集合が、他のあるＳi∋σkの持つＮ個の頂点の集合と共通のものとなる。
タイプ2のＳi∋σi,自身が持つＮ+1通りのＮ個の頂点の集合のうちN通りは、他のあるＳi∋σｋの持つＮ個の頂点の集合と共通のものとなるが、一つだけ、自身しか持たないＮ個の頂点の集合がある。
Ｓ3∋σはＪ∋σをタイプ1へＫ∋σをタイプ2へ対応させることができましたが、一般にＳi∋σも同じ様にタイプ1、タイプ2に分けることができます。
タイプ1へ分類されるＳi∋σ：自身の生成過程の2段階目で選択されたＮ個の頂点の集合が、ある2つの相異なるＳi-1∋σｊ,Ｓi-1∋σkそれぞれの頂点に含まれている。
タイプ2へ分類されるＳi∋σ：自身の生成過程の2段階目で選択されたＮ個の頂点の集合が、ある1つのＳi-1∋σｊの頂点にのみ含まれている。
ここで、重心細分を繰り返し行った時のＳi∋σのＮ+1個の頂点それぞれに次の規則に従い数字をつけます。
Ｓi∋σの頂点aijを、Ｓ1上の座標で表現したときaij＝ｂ1a1.1+ｂ2a1.2+ｂ3a1.3+-----bna1.ｎ+ｂｎ+1a1.n+1（0≦ｂi≦1|i=1～ｎ+1）
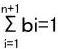
a1.iの係数ｂiで0≠ｂiとなっているｂiのiをaijに対応させます。0≠ｂiを満たすiが複数ある場合にはその中から任意のiを1つ選んで対応させます。
例えば、aij＝ｂ1a1.1+ｂ2a1.2+ｂ3a1.3（0＜ｂi＜1|i=1,2,3）ｂ1+ｂ2+ｂ3＝1であれば1か2か3いずれかの数字をつけ、aij＝ｂ4a1.4+ｂ6a1.6（0＜ｂi＜1|i=4,6）ｂ4+ｂ6＝1であれば4か6の数字をつけるといった具合です。
つまり、各頂点を1～ｎ+1の自然数へ対応させる写像です。この写像をＦとします。Ｆ（aij）＝i(i=1～ｎ+1）
Ｓi∋σに対してこの写像を用いた場合Ｆは、σの持つＮ+1個の頂点（ai.j,ai.k,ai.l------ai.m,ai.n）に作用するものとして、
Ｆ（σ）＝（F(ai.j),F(ai.k),F(ai.l)------F(ai.m),F(ai.n)）＝（i1,i2,i3,i4・・・in+1）(iｋ=1～ｎ+1）
また、ある頂点aijがＫ個の相異なるＮ単体Ｓi∋σ1、Ｓi∋σ2、Ｓi∋σ3、・・・、Ｓi∋σkに含まれる時、
Ｆ（σ1）＝（F(ai.j)＝i1,F(ai.k),F(ai.l)------F(ai.m),F(ai.n)）
Ｆ（σ2）＝（F(ai.j)＝i2,F(ai.o),F(ai.p)------F(ai.q),F(ai.r)）
Ｆ（σ3）＝（F(ai.j)＝i3,F(ai.s),F(ai.t)------F(ai.u),F(ai.v)）
・
・
・
Ｆ（σk）＝（F(ai.j)＝ik,F(ai.w),F(ai.x)------F(ai.y),F(ai.z)）
i1＝i2＝i3＝・・・＝iｋ
そして、集合Ｔi＝{Ｆ（σ）|σ＝全てのＳi∋σ} この様に集合Ｔiを定めると、次の補題が成り立つことが分かります。
シュペルナーの補題、任意のiについてＴi∋Ｆ（σk）が1～ｎ+1の全てを元としてもつＳi∋σkが奇数個存在する。
証明 以下、このような1～ｎ+1の全てを元としてもつＴi∋Ｆ（σo）の逆像σoを完全なＮ単体と呼ぶ。
あるＳi∋σoのＦ（σo）＝（i1,i2,i3,i4・・・in+1）からＮ個の元ik(ik=1～ｎ+1）を選択する。その選択の仕方はＮ+1通りあるが、その中で1～ｎの全てを元として持つ場合を数える。これは、0か1か2の場合があり得る。例えばその場合の数がｋならばＳi∋σoは、完全なＮ-1辺単体をｋ個持つこととなる。
ここで、次のような規則によって完全なＮ-1辺単体の数え上げを行う。
各Ｓi∋σがもつ完全なＮ-1辺単体の数を足して、その合計値を求める。 各Ｓi∋σが持つ完全なＮ-1辺単体の数は、0か1か2のいずれかとなるが、1の場合には、そのＳi∋σが完全なＮ単体である事を意味している。したがってＳiが完全なＮ単体を奇数個含めばこの合計値は奇数となり、Ｓiが完全なＮ単体を偶数個含めばこの合計値は偶数となる。今度は、あるＳi∋σに含まれるあるＮ個の頂点の集合を基準にして合計値を求める。Ｎ個の頂点の集合には、ある2つの相異なるＮ単体Ｓi∋σi,
Ｓi∋σｋに含まれる場合とある1つのＳi∋σにしか含まれない場合があります。このことから、
式、1（ある2つの相異なるＮ単体Ｓi∋σi,Ｓi∋σkに含まれる完全なＮ-1辺単体の数）×2+（ある1つＳi∋σにのみ含まれる完全なＮ-1辺単体の数）×1
という計算によっても求めたい合計値が得られます。つまり、ある1つのＳi∋σにのみ含まれる完全なＮ-1辺単体の数が奇数個存在することを示せばよいという事です。この事を帰納法によって示します。
まずは、1単体（線分）の重心細分です。下図では、1単体（a1,a2）を2回重心細分したときの推移を表現しています。
2回の重心細分によって頂点はa1,a2,a3,a4,a5の5つになりました。この5つの各頂点に上述の規則によって1か2の数字を対応させると、
a1→1、a2→2、a3→1か2、a4→1か2、a5→1か2 となります。すると4つの1単体は（a1,a4）→（1,1）か（1,2）、（a4,a3）→（1,1）か（1,2）か（2,1）か（2,2）
（a3,a5）→（1,1）か（1,2）か（2,1）か（2,2）、（a5,a2）→（1,2）か（2,2） ここでの完全なＮ-1辺単体とはＦ（ai)＝1となるai（i＝1～5）のことです。
頂点a1は端点であるため、1単体（a1,a4）にのみ含まれています。一方頂点a3,a4,a5は、端点ではないため2つの1単体に含まれます。したがって、式、1により
1単体（線分）では、補題が成り立つ事が分かります。
Ｎ-1では、補題が成り立つと仮定をし、Ｎでも成り立つことを示します。
下の表は、Ｓ1の重心細分の過程を3段階目の途中まで切り取ったものです。2段階目にＮ個の頂点を選択する際a1.n+1以外の頂点を選択したため1段階目を無視すれば2段階目以降は、Ｎ-1単体の重心細分と全く同じあることが分かります。
1段階目
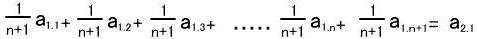この計算により新たに頂点a2.1が生成されました。2段階目↓（a1.1,a1.2,a1.3-----a1.n,a1.n+1)からｎ個の頂点を選択する。（ｎ+1通りの場合がありますが、ここでは例としてa1.n+1以外の頂点を選択します。）
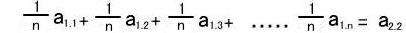この計算により新たに頂点a2.2が生成されました。
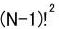個のΔの集合をＰ3とし、以下同様にＰi-1の全てΔそれぞれの重心細分によって生成されたΔの集合をＰiとする。すると、Ｐi=Ｌiである事が分かる。したがって、帰納法の仮定と式、1によりＮでも補題が成り立つ。