どれだけでしょう?
この問題は、ビュフォンの針の問題での期待値を使った解法を応用することで解くことができます。
問題文では、直径3cmの円形の物体とありますが問題を解くにあたってまず1辺1cmの正方形をN回落として十字にかかった数を考えます。
この数をM1として
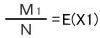 とする。さらに、E(X1)を正方形の面積で割ると次式になります。
とする。さらに、E(X1)を正方形の面積で割ると次式になります。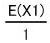
今度は、縦が1cm横が2cmの長方形で考えます。この長方形をN回落として十字にかかった数をM2とする。
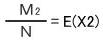 としてE(X2)をこの長方形の面積で割ると次式になります。
としてE(X2)をこの長方形の面積で割ると次式になります。 ビュフォンの針の応用問題
一辺10cmのタイルがまんべんなく敷き詰められた床に、直径3cmの円形の物体を落とします。この円形が、タイルの十字のところにかかっている確率は
どれだけでしょう?
この問題は、ビュフォンの針の問題での期待値を使った解法を応用することで解くことができます。
問題文では、直径3cmの円形の物体とありますが問題を解くにあたってまず1辺1cmの正方形をN回落として十字にかかった数を考えます。
この数をM1として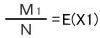 とする。さらに、E(X1)を正方形の面積で割ると次式になります。
とする。さらに、E(X1)を正方形の面積で割ると次式になります。
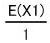
今度は、縦が1cm横が2cmの長方形で考えます。この長方形をN回落として十字にかかった数をM2とする。
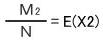 としてE(X2)をこの長方形の面積で割ると次式になります。
としてE(X2)をこの長方形の面積で割ると次式になります。
![]()
1×2の長方形は1×1の正方形が2個並んでいるとみなせます。これを右側の正方形、左側の正方形とに分けて考えます。
N回落とした時左側の正方形が十字にかかった数を無視すれば十字にかかった数はM1となります。
同様に右側の正方形が十字にかかった数を無視しても十字にかかった数はM1となります。
したがって、M2=2×M1 であり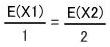 となります。
となります。
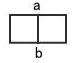 ※連続確率の問題では線分abに十字がかかる確率は0とみなせます。また、この線分abの面積も0です。(詳しくは最後に説明します。)
※連続確率の問題では線分abに十字がかかる確率は0とみなせます。また、この線分abの面積も0です。(詳しくは最後に説明します。)
次は、1辺の長さが0.5cmの正方形を考えます。この正方形N回落として十字にかかった数をM3とし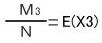 とします。
とします。
1辺の長さが1cmの正方形は1辺の長さ0.5cmの正方形が4つ並んだものとみなせます。したがって、
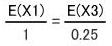
さらに、図の様なL字型の図形で考えてみます。
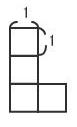 この図形をN回落として十字にかかった数ををM4とし、
この図形をN回落として十字にかかった数ををM4とし、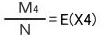 とします。
とします。
この場合は、1辺の長さ1の正方形が4つ並んでいるとみなせるので
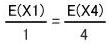
今度は、より多様な図形を扱えるように次の場合を考えます。
下図のように、正方形Sが円Cを内部に含んでいます。
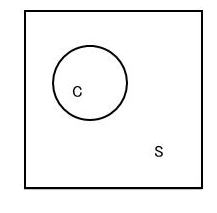
この時、正方形SをN回落としてSが十字にかかった数をMsとし、円Cが十字にかかった数をMCとすれば、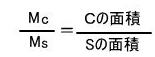 したがって、
したがって、
 となります。
となります。
したがって、この式は図形の形にも面積によっても変わらない定数である事が分かります。
そこで、1辺が10cmの正方形で考えます。この正方形を落とすと必ず一か所タイルの十字にかかります。
したがって、この正方形をN回落として十字にかかった数を
M5とし、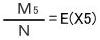 すれば、M5=Nから
すれば、M5=Nから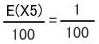 さらに、直径3cmの円をN回落として十字にかかった数をM6とし、
さらに、直径3cmの円をN回落として十字にかかった数をM6とし、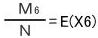 すると
すると
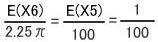 したがって、
したがって、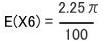
答え.![]() となります。
となります。
※ある面積を持った図形Aの定義可能な線分abが十字にかかる確率は0である。
この線分abを区間εで覆います線分abが十字にかかる確率をP(ab)、区間εが十字にかかる確率をP(ε)とするとP(ab)<P(ε)です。
線分の長さは1とします。長さが1ではなくても考え方は同じです。図の様にεは図形からはみ出ても構いません。
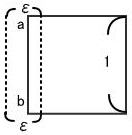
有限個の線分ab1,ab2,ab3,...abNに対しabを区間ε(1/2)で覆いab2を区間ε(1/4)でab3を区間ε(1/8)で以下同様にabiを区間ε![]() で覆います。
で覆います。
abiを覆うε![]() をεiとし図形Aが十字にかかる確率をP(A)図形Aの面積をL(A)とすると、
をεiとし図形Aが十字にかかる確率をP(A)図形Aの面積をL(A)とすると、
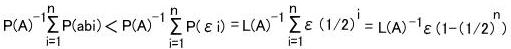
εはいくらでも小さくできるのでこの式は0になります。また線分の数が加算無限であっても上式のnが n=∞となり同様のことが言えます。
トップページへ