ランダムウォークの問題
1次元ランダムウォークにおいて原点(0)からスタートしKに触れるという事象が起きる前に-Kに触れ時刻NにMに至る道の数は何通りか?
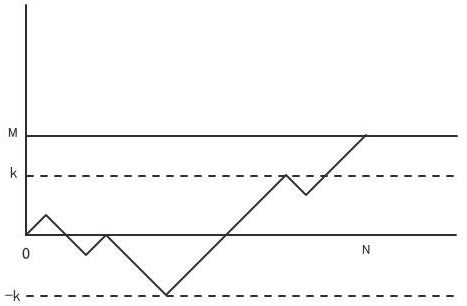
この問題は、反射原理と呼ばれる方法を繰り返し用いることで解くことができる。
まず、ランダムウォークが原点からスタートして-Kに触れてから時刻NにMへ至る道の数を調べる。
この道は、K~(N-M-K)のいずれかのステップで初めて-Kに触れるという事象が起こり、その後時刻NでMに至ると言う様に2つの段階に分けることができる。
したがって、P(P=K~(N-M-K))ステップで初めて-Kに触れてからMに至る道の数=Pステップで初めて-Kに触れる道の数×(N-P)ステップで-KからMに至る
道の数である。
原点からPまでの道の数をPU.PからMまでの道の数をPVとすると、原点からスタートして-Kに触れてから時刻NにMへ至る道の数は、PがK~(N-M-K)の場合に分ける
事ができるので、
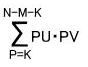 となる。
となる。
一方、-2Kからスタートして時刻NにMに至る道は、K~(N-M-K)ステップのどこかで初めて-Kに触れなくてはならない。
したがってこの道も、P(P=K~(N-M-K))ステップで初めて-Kに触れ、その後時刻NでMに至ると言う様に2つの段階に分けることができる。
-2KからPまでの道の数をPQとすると、-2Kからスタートして時刻NにMへ至る道の数は、PがK~(N-M-K)の場合に分ける事ができるので、
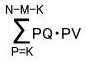 となる。
となる。
また、PQ=PU(P=K~(N-M-K))となっている。(PUのある1つの道のPまでの履歴が1-1-1+1-1-1-1ならば1と-1を交換した履歴
-1+1+1-1+1+1+1がPQのある1つの道のPまでの履歴に対応しこの対応は1対1であるため。)したがって、
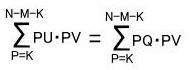 これを、反射原理と言います。
これを、反射原理と言います。
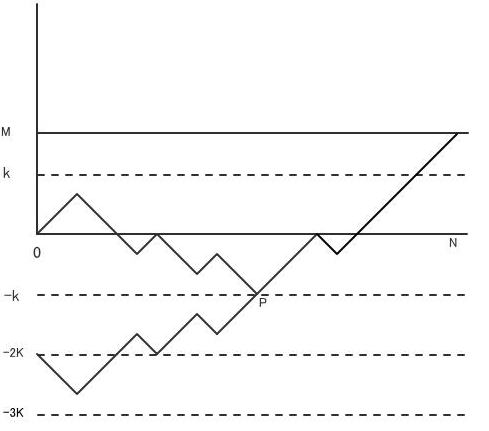
-2Kからスタートして時刻NにMに至る道には、-Kに触れるという事象が起こる前に-3Kに触れるという事象が起こっている場合がある。
この場合は、Pに至るまでの履歴の1-1を交換し原点からスタートした場合に変換すると、-Kに触れるという事象が起こる前にKに触れその後Mに触れるという
事象に対応している。
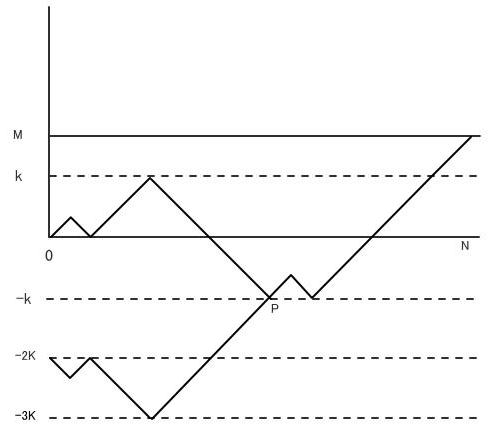
したがって、これだけでは問題を解くにあたって不十分です。
ここで問題解くために必要な記号の定義をします。
まず、-2Kからスタートして時刻NにMに到達する道の集合をA1、A1の道で-Kに触れるという事象が起こる前に-3Kに触れるという道の集合をÀ1とする。
さらに、-4Kからスタートして時刻NにMに到達する道の道の集合をA2、A2の道で-3Kに触れるという事象が起こる前に-5Kに触れるという道の集合をÀ2とする。
以下同様に、-2iKからスタートして時刻NにMに到達する道の集合をAi、Aiの道で(-2i+1)Kに触れるという事象が起こる前に前に(-2i-1)Kに触れるという
道の集合をÀiとする。
次の写像を定義する。写像Fを、Aiに含まれる道Ai∋xに対して作用させると、xが初めて(-2i+1)Kに触れるまでの履歴の1と-1を交換する。
すると、反射原理によって F(Ai)⊃Ài-1. がいえる。
そして、iを大きくしていくとあるAiでÀiが存在しないものがでてくる。[NステップでMに到達可能だが、(-2i-1)Kに触れるという事象が起こると
NステップではMに到達不可能となるi] このiをZとする。Z=[(N-M)/2K]((N-M)を2Kで割った数から小数点以下を切り捨てた数)
問題の答えは、
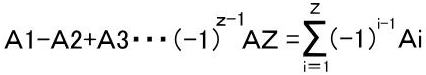 という交代和になることが分かります。
という交代和になることが分かります。
この問題は、次の問題に応用できます。
原点からスタートしたランダムウォークがDにもLにも触れずに時刻NにMに到達する道の数は?
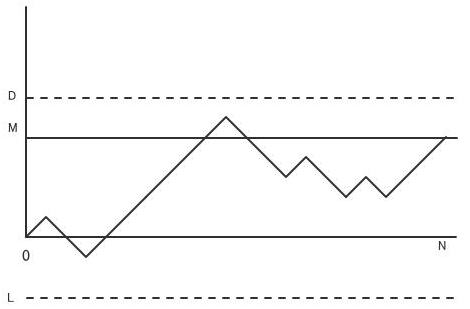
この問題の答えは、原点からスタートしたランダムウォークが時刻NにMへ到達する道の数(これをTとする。)
原点からスタートしたランダムウォークがDに触れてから時刻NにMへ到達する道の数(これをOとする。)、同じくLに触れてから時刻NにMに到達する道の数
(これをPとする。)、DとL両方に触れてから時刻NにMに到達する道の数(これをQとする。)この様にT,O,P,Q定めると次の様になります。
原点からスタートしたランダムウォークがDにもLにも触れずに時刻NにMに到達する道の数=T-O-P+Q
Oについては、原点からスタートしたランダムウォークが時刻NにD+(D-M)へ到達する道の数と同じです。Pについては、-2Lからスタートしたランダムウォークが時 刻NにMへ到達する道の数と同じです。
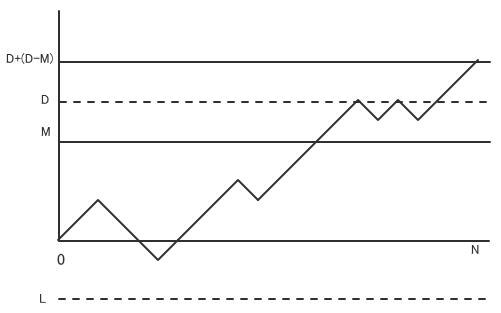
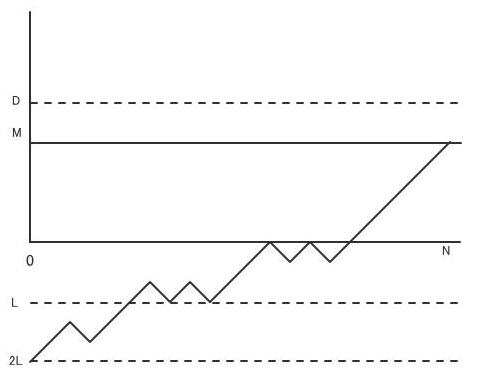
Qについては、Dに触れる前にLに触れその後Dに触れる場合とLに触れる前ににDに触れその後Lに触れる場合の二通りがあります。
これらの道の数は、原点(0)からスタートしKに触れるという事象が起きる前に-Kに触れ時刻NにMに至る道の数を導いた時と同様の議論によって導く事が
出来ます。
トップページへ

 となる。
となる。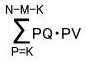 となる。
となる。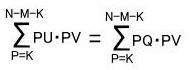 これを、反射原理と言います。
これを、反射原理と言います。

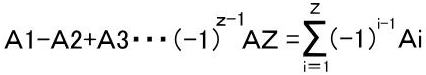 という交代和になることが分かります。
という交代和になることが分かります。

